密码学(cryptology)可以分成两大部分,一部分是密码分析学(cryptanalysis),它侧重于利用各种手段(包括但不仅限于理论分析)进行攻击。但是我们要讲的是另一部分,也就是下面要说的密码学(cryptography),它侧重于用数学的手段去研究信息安全,范围涵盖信息机密性,数据完整性,身份认证和消息认证等等。
其实说起密码学,很多人最先想到的可能是破译密码,或者盗号(?),然后学习一段时间后发现,这说的根本不是一回事儿!首先纠正一个误区,就是我们生活中常说的“密码”,比如说登录各大网站时使用的那种,其实不是密码学里指的密码,而是“口令”(password)。其次,学习密码学真的不会让你具备盗号的能力,所以放弃幻想,拥抱现实。我们先从密码学的历史谈起,然后再正式地说一说密码学到底是怎么进行“系统化”研究的。
古典密码学
密码学(cryptography)这个单词其实就很好地解释了密码学的历史。在希腊语里,kryptos 表示“隐藏的”,graphein 表示“书写”,因此连起来会发现密码学最早表达的意思是“隐写术”,而它出现的动机也很明确,就是为了双方能安全而隐秘地进行通信,方法就是一方写好要通信的信息后,用某种特殊药水把它隐藏起来,将纸张变得好像没有写过文字一样。而另一方拿到这张纸后,就用相应的特殊药水处理一遍,还原出最初写在纸上的明文信息。它的设计目的在于,让没有相应特殊药水的人很难从那张纸上获得任何明文信息,从而保证通信的安全。
历史上另一个比较著名的古典密码为凯撒密码(Caesar’s cipher)。传闻是凯撒大帝用来给将军传递命令的。它的加密方式是:对明文中的每个字母都进行一次 3 位的循环右移。拿英语来举例子,明文中的任何字母 a 都会被替换成字母 d,而字母 b 会被替换成字母 e,以此类推,最后字母 z 会被替换成字母 c。比如明文“hello”会被加密成密文“khoor”。
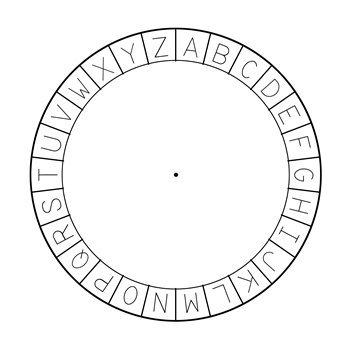
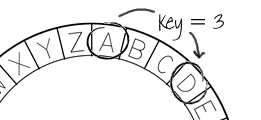
但是这个密码有一个问题,就是如果某个人知道这个密码是这样设计的,那么他就可以轻而易举地破译任何他截获的密文,方法很简单,就是把密文中的每个字母都进行一次3位的循环左移。看到这里你可能会问,那我把这个设计方式也保密不就行了?这样别人拿到密文也不知道我是怎么加密的,他看到的只是一堆无序的字母。在很长的一段时间里,人们确实也是这么做的,就是只把加密解密方式告诉通信双方而对其他人严格保密。可是事实证明,这样的方式是脆弱的。很多密码因为偶然泄露了加密方式之后就变得不堪一击,继而许多用这种加密方式加密的密文都被破译了。最终,一个叫 Kerckhoff 的人在19世纪石破天惊地提出:“密码设计不能再这样下去了!为了安全我们要最大限度地公开!”
Kerckhoff 原理
“为了安全而最大限度地公开”?这意味着一个密码构造的所有细节都应该被全部公开,包括公开给那些想要攻击这个构造的人,也就是说,一个安全的密码构造在使用时只有通信双方的密钥是保密的。
这仿佛一个悖论。可是这个观点如今是公认的密码设计的准则,甚至被认为是从古典密码学到现代密码学的转变的标志之一(另一个标志就是引入系统化分析方法),让密码学从艺术变为科学。看似荒诞的假说背后,其实仔细想想就能找到答案。
我们要明确一点,密码学虽然是个比较理论的学科,但是它的最终目的还是用于实践的。因此在密码设计时,就不得不考虑现实的情况。而 Kerckhoff 原理在实际中的合理性主要基于以下两点:
第一, 显而易见的,对一个密钥(通常较短)保密远比对复杂的整个机制保密容易得多。因为对于许多用户来说,共用同一个加密机制而分配不同的密钥更合理,否则就得每建立一个通信连接就换一种新的机制,这无疑是复杂且不现实的。
第二,即使保密的信息被暴露,那么更换密钥远比更换使用的加密机制要方便,尤其对于那些大型的使用场景来说。
下面带着 Kerckhoff 原理,我们来正式地表述一个加密设计。
认识一些术语
首先,我们还是以双方通信做为我们的应用场景,消息发送方我们戏称为 Alice,接受方则被戏称为 Bob。在这里我们假设 Alice 和 Bob 已经在这次通信前从所有可能的密钥取值集合(称为密钥空间 $\mathcal{K}$)中商量好了选一个确定的密钥 $k$(key)。他们具体是如何确定这个共享的密钥的我们暂时不考虑,只需要知道 boom 很神奇的(或许是通过面对面交流)他们就有了一个非常安全的不为人所知的密钥。
现在 Alice 想要用这个共享密钥 $k$ 给 Bob 发送一条消息 $m$(message,或称明文 plaintext),她首先在本地使用加密算法 $Enc$(Encryption)和密钥 $k$ 来生成消息 $m$ 对应的密文 $c$(ciphertext)。然后她使用公用信道把 $c$ 发送给 Bob。这里说的公用信道其实就是指不安全信道,即存在监听者 Eve(可能来源于窃听者的英文 eavesdropper)能够截获信道上的比特流,因此 Eve 也会知道 $c$。信道另一端的 Bob 收到了 $c$ 后,就在本地用解密算法 $Dec$(Decryption)和密钥 $k$ 来还原出密文 $c$ 对应的明文 $m$。这样 Alice 和 Bob 就完成了一次通信。
再次重申,根据 Kerckhoff 原理,加密算法 $Enc$ 和解密算法 $Dec$ 是完全公开的,也就是说,任何人只要有 $k$ 和 $m$ 都能使用 $Enc$ 来计算 $c$,任何人只要有 $k$ 和 $c$ 都能使用 $Dec$ 来计算 $m$!
重审经典古典密码
有了上述关于术语和 Kerckhoff 原理的介绍,我们可以数学化地表示凯撒密码了。
我们给英文字母 a~z 编码,分别为 0~25,这样对于明文中每一个字母,它的加解密如下:
注意,$Enc$ 和 $Dec$ 的参数中之所以没有密钥 $k$,是因为凯撒密码已经规定了密钥就是 3,根据 Kerckhoff 原理,这是一个公开值。
所以,看到这里我们就能发现,在现代密码学的设定下,凯撒密码简直就是裸奔呐!没有任何隐秘性和安全性可言。
或许,我们可以改进一下?把密钥加上,不再规定 $k$ 是 3 了,而是 0~25 之间的任何一个数。这样密钥空间就从原来的 $\{3\}$ 变为了 $\{0, 1, \cdots, 25\}$。这就是移位密码(shift cipher),它的加解密如下:
虽然它看上去比凯撒密码安全一些,不过很不幸它在穷举攻击前不堪一击。攻击者只需要穷举 $k \in \{0, 1, \cdots, 25\}$ 分别对 $c$ 试图解密,直到解密出的 $m$ 是一段可以阅读的文字。
或许,再改进一下?我们这次不再简单地让 a~z 移位相同的距离了,而是对每个不同的字母都取定一个对应的字母。同时为了解密的正确性,不同的字母对应不同的加密字母。因此密钥就是一张置换表,比如:把 a 对应 x,b 对应 e,c 对应 u 等等。这就是置换密码(substitution cipher)。
这一次我们有了很大进步,我们一举把密钥空间大小 $|\mathcal{K}|$ 从移位密码里的 26,提高到现在的 26!(这里感叹号是表示阶乘,$26! \approx 2^{88}$)。安全感满满的。但是依旧很不幸的是,这个密码也是不安全的!原因在于它是确定型(deterministic)加密的,也就是说消息 $m$ 中任何相同的字母,虽然攻击者不知道它们对应的加密字母是什么,但攻击者可以确定这些加密字母都是同一个字母,比如说明文“hello”在这里会被加密成“kdoof”,攻击者拿到这个密文后,就可以猜测它是一个五个字母的单词而且倒数二、三位置是两个相同的字母,符合这个条件的英文单词并不多,因此攻击者可以很快地就破译出这个密文对应的明文是“hello”。
把上述攻击一般化,攻击者可以统计密文中每个字母的出现频率。又由于一段文字中,不同字母并不是随机出现的,有一些字母如 e,a,t 就比另一些字母如 j,z 出现得更加频繁。如果攻击者拿到一段密文,统计发现 d 出现的次数最多,那么他就可以认为 d 就是字母 e 的加密结果。依此类推可以破译出如字母 a,t 的加密结果。部分破译后,攻击者又可以通过文章里常出现的比如 the,we,you 等单词,推测出其他字母的加密结果。因此这个密码的实际密钥空间并没有 26!,而是可以用已有的语言学知识来缩小搜索空间,也可以很容易地全部破译。
现代密码学的系统化分析
上面说到,除了 Kerckhoff 原理,从古典密码学到现代密码学还有一个重大的改变,就是引入了系统化的分析工具。比如在上一节的分析中我们一直在强调的密钥空间大小也是其中的一环。这一节我们就来讲一讲这些系统化的分析。
首先我们遇到的第一个急需解决的尴尬境地是:怎么定义“安全”?毕竟如果这个不明确的话,我们在设计时怎么知道设计出来的构造是不是安全的?前面我们分析了那么多,指出比如凯撒密码,移位密码,置换密码都是不安全的,这是因为我们指出了它们的缺陷并给出了攻击方法。但是如果一个密码构造,我们暂时还没有找出破解它的办法,那么就一定能说这个构造是安全的吗?要知道,在很长一段时间内,凯撒密码也曾被认为是安全的呢!因此这种安全定义肯定不合理。更好的定义是要求攻击者无法从密文中得到任何有关明文的信息,而不对攻击者的策略(strategy)做任何假设,因为现实情况就是攻击者会用各种我们想到的和想不到的方式来试图攻击我们的密码构造。当然,不对攻击者的策略做假设不代表不对攻击者做限制。我们的安全性不可能是绝对安全的,而是对于具有某种能力(power)的攻击者的安全性,更术语一点,对攻击者能力的刻画我们称为威胁模型(threat model)。威胁模型主要有仅密文攻击(ciphertext-only attack),已知明文攻击(known-plaintext attack),还有比较费解但其实非常常用的选择明文攻击(choosen-plaintext attack)和选择密文攻击(choosen-ciphertext attack)。这些在后面的内容中都会讲到。
其次,现代密码学一个非常显著的特点就是密码构造(安全性证明)是基于某个困难问题假设的。说它是“假设”是因为既不能证明它的正确性也不能证明它是错误的,但是它被公认为是正确的。这也是计算机科学中非常尴尬的一点,就像 P/NP 问题那样,虽然是计算复杂度理论的基石,可现在依然是未解决的状态。看到这里我们可能会有一个疑问:如果真的是这么尴尬的境地,我们避开它不就好了?为什么还要用它来构造我们的密码算法呢?我猜测这可能是因为,用这样的至今未解决的问题做为基础虽然看起来很冒险,可是恰恰是较安全的,因为的确没有人能解决它。还有一个原因就是,使用困难问题假设做为基础之后,我们就可以通过比较它们底层的困难问题假设来比较两个不同构造的安全性。除此之外,由于已经证明的密码构造的安全性几乎完全是基于其困难问题假设的,因此我们只需要检查这个困难问题有何进展就可以清楚地知道这个密码构造是否依然安全。
综上所述,一个现代密码构造的安全定义的完整表达是:在某困难问题假设成立的前提下,该密码学构造对于某个威胁模型是安全的。
当然,上述结论只是理论意义上的,在实际使用中,由于编程实现、操作不当等原因都有可能让理论上安全的密码构造变得不那么安全。同时做为结语,在看完这个介绍内容之后,即使我们以后什么都忘了,仍需要记住的是:不要轻易地试图自己构造密码算法!也不要通过隐藏构造细节来让构造变得安全(security by obscurity)!尽量使用已经标准化的通用的密码算法和实现!
参考资料
J. Katz and Y. Lindell. Introduction ro Modern Cryptography. Chapman and Hall/CRC Press, second edition, November 2014.